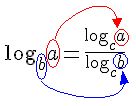Logaritimo(s)

Considerando a e b  dois números reais e positivos, sempre com a diferente de 0 , define-selogaritmo de b (logaritmando) na base a, qual número deve-se incluir no expoente de a afim de termos b como resultado.

Assim: a^x = b , então temos que 

Com as condições de .

I) , sendo que 3 é o logaritmo, 2 é a base e 8 é o logaritmando.
pois temos que 2³ = 8.

II) , sendo que –3 é o logaritmo, 3 é a base e 1/27 é o logaritmando.
pois temos que 3^-3 = 1/27 .

→ Antilogarítimo é definido como sendo: 
Exemplo:

I) 

Propriedades zero ( que são conseqüência direta da definição)

1º Propriedade (propriedade do produto).

2º Propriedade (propriedade do quociente).

3º Propriedade (propriedade da potência).

Conseqüência da 3º propriedade :

4º Propriedade (propriedade da mudança de base).

→ Colog, definição:

Mudança de base de Logaritmos

Em muitos casos na resolução de operações envolvendo logaritmos, é viável e se faz necessário a utilização de técnicas capazes de nos fornecer de forma precisa e direta o conjunto solução de uma questão, uma dessas “técnicas” é conhecido como mudança de base de um logaritmo, na qual veremos a seguir.

Vejamos:

Observe que inicialmente temos um logaritmo qualquer representado por uma base “b” e o logaritmando “a” , fazendo a mudança de base , vamos transformar esse logaritmo em um quociente de um logaritmo formado por um base “c” .Podemos perceber que tanto “a” quanto “b” passam a ser o logaritmando formado pela base “c”.

Para facilitar o entendimento da mudança de base, iremos aqui resolver alguns exercícios. Lembrando sempre que para que um logaritmo exista, sua base tem que ser maior que 0 e diferente de 1 (b>0 e b=/=1) e também é importante lembrar que seu logaritmando tem que ser maior que 0(a>0).

1) Calcule pela mudança de base o valor de  Log₄64 .

Podemos escrever que;

Log₄64 = log₂ 64 / log₂ 4

Calculando separadamente, temos;

Log₂64 = 2^x = 2⁶; x=6

Log ₂4 = 2^x = 2²;  x=2

Portanto, x =6/2 = 3

Para provarmos essa técnica poderíamos conferir a resposta pela definição do logaritmo, sendo 64 um múltiplo de 4, sua forma fatorada é   64= 4³

Portanto  Log₄64 = x  ;  4^x=4³, x=3

2) Sabendo-se que log₁₀ 2 =0,301  e log₁₀ 3=0,477 , pede-se. Calcule o valor de  Log₉512

Podemos escrever que;

Log₉512= log₁₀512/log₁₀9

Calculando separadamente, temos;

Log ₁₀512= Log ₁₀2⁹= 9 x log₁₀2 =9×0, 301=2,709

Log₁₀9= Log₁₀3²= 2xlog₁₀3=2×0, 477=0, 954

Reescrevendo (Efetuando o quociente);

Log₉512= 2,709/0,954 =2,839(Resultado aproximado).

Cologaritmo

O estudo do cologaritmo tem sua  principal “raiz” o estudo dos logaritmos  e suas propriedades operacionais, apesar de pouco cobrado em concursos e vestibulares, não diminui de forma alguma seu grau de importância.

Define-se cologaritmo de um número real pelo oposto de seu logaritmo. Vejamos a seguir sua definição algébrica;

Colog _b a = – log _b a

Desenvolvendo-se sua  definição matemática, a mesma poderia ser escrita da seguinte forma;

Colog_ba= log_ba^-1 ,ou seja, Colog _b a= log _b 1/a

Sabendo que o cologaritmo é um tipo “especial” de logaritmo, para que sua condição de existência seja satisfeita, devemos ter:

• b >0 e b ≠ 1 (base maior que zero e diferente de um)
• a > 0 (logaritmando maior que zero)

Consequentemente para resolvermos o cologaritmo devemos relembrar as principais propriedades operacionais de logaritmos.

1) Logaritmo de um produto ( O produto de um logaritmo é  igual a soma de seus logaritmos)

Log_c (a.b) = Log_ca + log_cb

2) Logaritmo de um quociente (O logaritmo de um quociente é igual a diferença dos logaritmos)

Log_c(a/b)= Log_ca – Log_cb

3) Logaritmo de uma potência ( O logaritmo de uma potência, é igual ao produto dessa potência pelo logaritmo)

Log_caⁿ = n . Log_ca

Sendo assim relembradas algumas operações com logaritmos conseqüentemente estamos aptos a resolver qualquer exercício de cologaritmo que é o que realmente nos interessa. Segue abaixo alguns exercícios para facilitar o entendimento do conteúdo.

1) Calcule o colog(2 . 3)

Lembrar que quando omitimos o valor da base, estamos trabalhando com a base decimal (10)

Resolvendo;

Colog₁₀(2.3) =colog₁₀1/2 + colog₁₀1/3 = -0,778

2) Calcule o colog₄64

Colog₄64= Log₄(1/64)=x

4^x=1/64

4^x=64^-1

4^x= (4³)^-1

X=-3

Através desse exemplo podemos ratificar a idéia que para resolver o cologaritmo , basta resolvermos o mesmo como se fosse um logaritmo normal, e na solução trocarmos o sinal do resultado (oposto do número)

3) Calcule o colog (2/3)

Colog₁₀2/3 = Log 2/3 =Log 2- Log3=-0,176= 0,176 (quando fazemos desse modo basta lembrar de trocar o sinal do resultado)

Exercícios – Logarito

Exercício 1: (FUVEST 2010)

A magnitude de um terremoto na escala Richter é proporcional ao logaritmo, na base 10, da energia liberada pelo abalo sísmico. Analogamente, o pH de uma solução aquosa é dado pelo logaritmo, na base 10, do inverso da concentração de íons H+. Considere as seguintes afirmações:

I. O uso do logaritmo nas escalas mencionadas justificase pelas variações exponenciais das grandezas envolvidas.

II. A concentração de íons H+ de uma solução ácida com pH 4 é 10 mil vezes maior que a de uma solução alcalina com pH 8.

III. Um abalo sísmico de magnitude 6 na escala Richter libera duas vezes mais energia que outro, de magnitude 3.

Está correto o que se afirma somente em:

Exercício 2: (UDESC 2008)

Sabendo que log₃(7x – 1) = 3 e que log₂(y³ + 3) = 7 pode-se afirmar que log_y(x² + 9) é igual a:

Exercício 3: (UFMG 2009)

Numa calculadora científica, ao se digitar um número positivo qualquer e, em seguida, se apertar a tecla log, aparece, no visor, o logaritmo decimal do número inicialmente digitado.

Digita-se o número 10.000 nessa calculadora e, logo após, aperta-se, N vezes, a tecla log, até aparecer um número negativo no visor. Então, é CORRETO afirmar que o número N é igual a:

Exercício 4: (UDESC 2008)

Se log_a b = 3 e log_ab c = 4, então log_a c é:

Exercício 5: (UFMS 2010)

Dado o sistema a seguir, e considerando log o logaritmo na base 10, assinale a(s) afirmação(ões) correta(s).

Gabarito: D,B,B,B, 1,8 e 16.