Pesquisar no site
Contato
Enquete
gostou do nosso blog?
Vetores
Vetor Unitário
Um vetor ![]() é unitário se |
é unitário se |![]() | = 1.
| = 1.
Versor
Versor de um vetor não nulo ![]() é o vetor unitário de mesma direção e mesmo sentido de
é o vetor unitário de mesma direção e mesmo sentido de ![]() .
.
Por exemplo, tomemos um vetor ![]() de módulo 3.
de módulo 3.
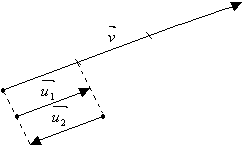
Os vetores ![]() e
e ![]() da figura são vetores unitários, pois ambos têm módulo 1. No entanto, apenas
da figura são vetores unitários, pois ambos têm módulo 1. No entanto, apenas ![]() tem a mesma direção e o mesmo sentido de
tem a mesma direção e o mesmo sentido de ![]() . Portanto, este é o versor de
. Portanto, este é o versor de ![]() .
.
Vetores Colineares
Dois vetores ![]() e
e ![]() são colineares se tiverem a mesma direção. Em outras palavras:
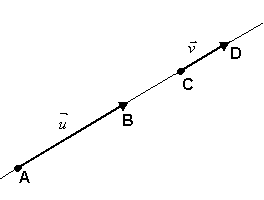
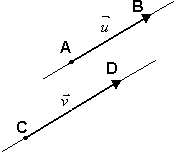
são colineares se tiverem a mesma direção. Em outras palavras: ![]() e
e ![]() são colineares se tiverem representantes AB e CDpertencentes a uma mesma reta ou a retas paralelas.
são colineares se tiverem representantes AB e CDpertencentes a uma mesma reta ou a retas paralelas.
Vetores Coplanares
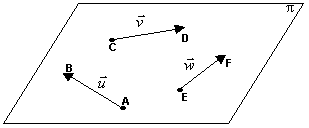
Se os vetores não nulos ![]() ,
, ![]() e
e ![]() (não importa o número de vetores) possuem representantes AB, CD e EF pertencentes a um mesmo plano p, diz-se que eles são coplanares.
(não importa o número de vetores) possuem representantes AB, CD e EF pertencentes a um mesmo plano p, diz-se que eles são coplanares.
Dois vetores ![]() e
e ![]() quaisquer são são sempre coplanares, pois podemos sempre tomar um ponto no espaço e, com origem nele, imaginar os dois representantes de
quaisquer são são sempre coplanares, pois podemos sempre tomar um ponto no espaço e, com origem nele, imaginar os dois representantes de ![]() e
e ![]() pertencendo a um plano p que passa por este ponto.
pertencendo a um plano p que passa por este ponto.
Três vetores poderão ou não ser coplanares.
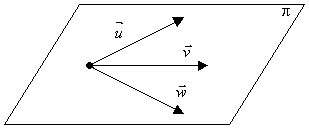
![]() ,
, ![]() e
e ![]() são coplanares
são coplanares
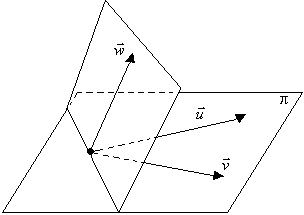
![]() ,
, ![]() e
e ![]() não são coplanares.
não são coplanares.
Grandezas Vetoriais
Grandezas físicas que não ficam totalmente determinadas com um valor e uma unidade são chamadas de grandezas vetoriais. As grandezas que ficam totalmente expressas por um valor e uma unidade são chamadas de grandezas escalares. Como exemplo de grandeza escalar temos a massa. Já as grandezas vetoriais, para que fiquem totalmente definidas necessitam de:
* Um Valor (módulo);
* Uma Unidade;
* Uma Direção;
* Um sentido.
Como exemplos de grandeza vetorial temos:
Um vetor por sua vez tem três características: módulo, direção e sentido.
Para representar graficamente um vetor usamos um segmento de reta orientado.
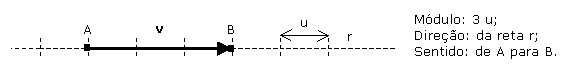
O módulo do vetor, representa numericamente o comprimento de sua seta. No caso anterior, o módulo do vetor é igual a distância entre os pontos A e B, que por sua vez vale 3 u.
Para indicar vetores usamos as seguintes notações:
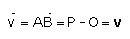
O módulo de um vetor é indicado utilizando-se duas barras verticais.
|A| (Lê-se: módulo de A)
Adição de Vetores
Podemos somar dois ou mais vetores, para obter um vetor soma.
Regra do polígono:
Ligam-se os vetores origem com extremidade. O vetor soma é o que tem origem na origem do 1º vetor e extremidade na extremidade do último vetor.
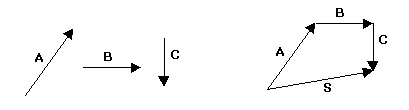
Subtração de Vetores
Para subtrair dois vetores adicionamos um deles ao oposto do outro.
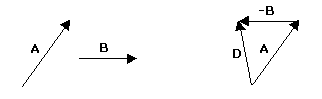
Decomposição de Vetores
A decomposição de vetores é usada para facilitar o cálculo do vetor resultante.
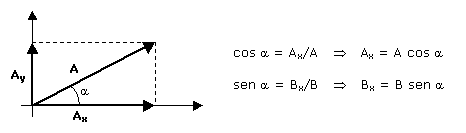
Seja um vetor R resultado da seguinte operação: R = A + B
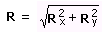
Onde:
Rx = Ax + Bx
Ry = Ay + By
aqui é matemática.
